En física, velocidad es la magnitud física que expresa la variación de posición de un objeto en función del tiempo, o distancia recorrida por un objeto en la unidad de tiempo. Se suele representar por la letra  . La velocidad puede distinguirse según el lapso considerado, por lo cual se hace referencia a la velocidad instantánea, la velocidad promedio, etcétera. En el Sistema Internacional de Unidades su unidad es el metro por segundo
. La velocidad puede distinguirse según el lapso considerado, por lo cual se hace referencia a la velocidad instantánea, la velocidad promedio, etcétera. En el Sistema Internacional de Unidades su unidad es el metro por segundo  ó
ó 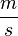 .
.
 . La velocidad puede distinguirse según el lapso considerado, por lo cual se hace referencia a la velocidad instantánea, la velocidad promedio, etcétera. En el Sistema Internacional de Unidades su unidad es el metro por segundo
. La velocidad puede distinguirse según el lapso considerado, por lo cual se hace referencia a la velocidad instantánea, la velocidad promedio, etcétera. En el Sistema Internacional de Unidades su unidad es el metro por segundo  ó
ó 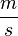 .
.
En términos precisos, para definir la velocidad de un objeto debe considerarse no sólo la distancia que recorre por unidad de tiempo sino también la dirección y el sentido del desplazamiento, por lo cual la velocidad se expresa como una magnitud vectorial.
La velocidad media o velocidad promedio informa sobre la velocidad en un intervalo dado. Se calcula dividiendo el desplazamiento (delta x) por el tiempo transcurrido (delta t):
Por ejemplo, si un objeto ha recorrido una distancia de 1 metro en un lapso de 31,63 segundos, el módulo de su velocidad media es:
Al módulo de la velocidad se le llama rapidez.
VELOCIDAD INSTANTANEA
Informa sobre la velocidad en un punto dado.
En forma vectorial, la velocidad es la derivada (tangente) del vector posición respecto del tiempo:
 \vec v= \frac {ds}{dt} \ \vec u_t = \frac {d{\vec r}}{dt}</math>
\vec v= \frac {ds}{dt} \ \vec u_t = \frac {d{\vec r}}{dt}</math>
donde 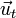 es un versor (vector de módulo unidad) de dirección tangente a la trayectoria de cuerpo en cuestión y
es un versor (vector de módulo unidad) de dirección tangente a la trayectoria de cuerpo en cuestión y 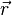 es el vector posición, ya que en el límite los diferenciales de espacio recorrido y posición coinciden.
es el vector posición, ya que en el límite los diferenciales de espacio recorrido y posición coinciden.
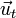 es un versor (vector de módulo unidad) de dirección tangente a la trayectoria de cuerpo en cuestión y
es un versor (vector de módulo unidad) de dirección tangente a la trayectoria de cuerpo en cuestión y 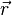 es el vector posición, ya que en el límite los diferenciales de espacio recorrido y posición coinciden.
es el vector posición, ya que en el límite los diferenciales de espacio recorrido y posición coinciden.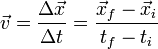

No hay comentarios:
Publicar un comentario